Object Classes¶
The fundamental classes that functions are built up from are described below.
Most of these classes are defined in mathics.core.element or mathics.core.expression.
Class Diagram for Some of the Classes¶
Below is a UML 2.5 Class diagram for some of the classes described below:
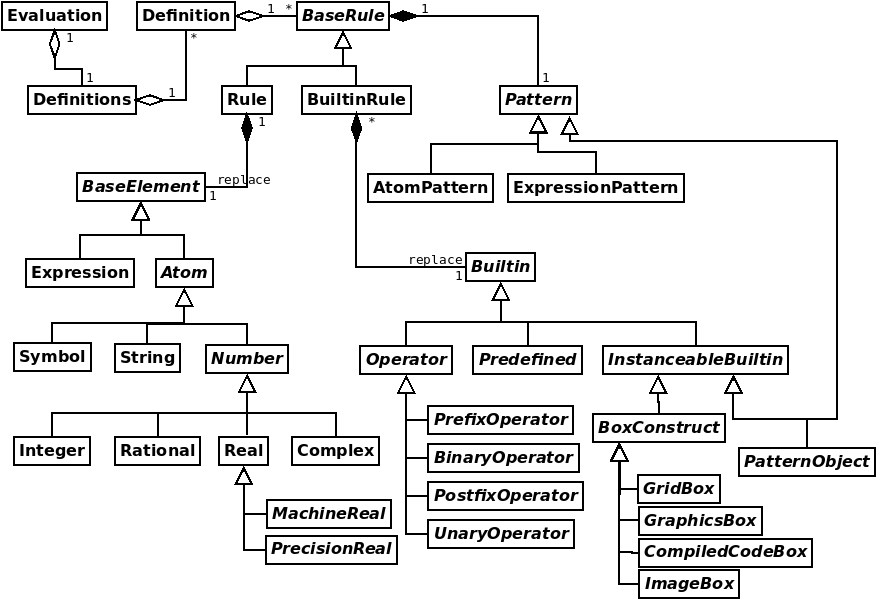
A Class name that begins with Base is a Virtual class.
Mathics3 Core Classes¶
Atom Class¶
Recall that an Expression to be evaluated is initially a kind of M-expression,
an object in the Expression class, where each list item is either itself
an Expression or an object in a class derived from Atom.
The Atom class we encountered earlier when describing the nodes
that get created initially from a parse. Those were:
NumberStringSymbolFilename
Atoms here is from module mathics.core.parse.ast
However this is converted in mathics.core.parser.convert.Converter.convert()
into another kind of expression where Number is replaced by a more
specific kind of number like Integer, or Real.
There are a few other kinds of Atoms or fundamental objects like:
ByteArrayCompiledCodeComplexDispatchImage
In general, atoms are objects might have an underlying internal representation with no user-visible subparts that can be pulled out using Part[].
In Mathics, the function AtomQ[] will tell you if something is an Atom, or can’t be subdivided into subexpressions.
Some examples:
(* Strings and expressions that produce strings are atoms: *)
>> Map[AtomQ, {"x", "x" <> "y", StringReverse["live"]}]
= {True, True, True}
(* Numeric literals are atoms: *)
>> Map[AtomQ, {2, 2.1, 1/2, 2 + I, 2^^101}]
= {True, True, True, True, True}
(* So are Mathematical Constants: *)
>> Map[AtomQ, {Pi, E, I, Degree}]
= {True, True, True, True}
(* A 'Symbol' not bound to a value is an atom too: *)
>> AtomQ[x]
= True
(* On the other hand, expressions with more than one 'Part' after evaluation, even those resulting in numeric values, aren't atoms: *)
>> AtomQ[2 + Pi]
= False
(* Similarly any compound 'Expression', even lists of literals, aren't atoms: *)
>> Map[AtomQ, {{}, {1}, {2, 3, 4}}]
= {False, False, False}
(* Note that evaluation or the binding of "x" to an expression is taken into account: *)
>> x = 2 + Pi; AtomQ[x]
= False
(* Again, note that the expression evaluation to a number occurs before 'AtomQ' evaluated: *)
>> AtomQ[2 + 3.1415]
= True
BaseElement Class¶
A Mathics3 M-expression is the main data structure which evaluation is
performed on. An M-expression is, in general, a tree. The nodes of this
tree come from the BaseElement class. Note that element in
addition to being a BaseElement are an Atom as well. In other words,
an Atom is a subclass of BaseElement.
The other subclass of BaseElement is an Expression.
Note as the prefix Base implies, a BaseElement is a virtual class.
Definition Class¶
A Definition is a collection of Rules and attributes which are associated with a Symbol.
A Rule is internally organized in terms of the context of application in
OwnValues,UpValues,Downvalues,Subvalues,FormatValues, etc.
Definitions Class¶
The Definitions class hold state of one instance of the Mathics interpreter is stored in this object.
The state is then stored as Definition object of the different symbols defined during the runtime.
In the current implementation, the Definitions object stores Definition s in four dictionaries:
builtins: stores the definitions of the
Builtinsymbolspymathics: stores the definitions of the
Builtinsymbols added from pymathics modules.user: stores the definitions created during the runtime.
definition_cache: keep definitions obtained by merging builtins, pymathics, and user definitions associated to the same symbol.
Expression Class¶
An Expression object the main object that we evaluate over. It represents an M-expression formed from input.
Although objects derived from Atom, e.g. symbols and integers, are
valid expressions, this class describes compound expressions, or
expressions that are more than a single atom/element. So in contrast to an
object of type Atom, an Expression object is some sort of
structured node that as in Mathics3 itself, has a Head (function
designator) and a Rest (or arguments) component.
Symbol Class¶
Just above the Atom class is the Symbol which is an atomic element of an Expression.
See Atomic Elements of Expressions.
As born from the parser, Symbols start off like Lisp
Symbols. Following WL, Mathics3 has about a thousand named characters,
some common ones like “+”, “-”, and some pretty obscure ones. After
parsing, each of these can be incorporated into a Symbol object. But
in the evaluation process in conjunction with the Definitions
object that is in the evaluation object, these symbols get bound to
values in a scope, and then they act more like a programming language
variable. The Symbol class described here has fields and properties
that you of the kind that you’d expect a variable in a programming
language to have.
Classes for Defining Builtin Functions¶
Builtin class¶
A number of Mathics3 variables and functions are loaded when Mathics3 starts up,
thousands of functions even before any Mathics3 packages are loaded. As with other Mathics3 objects
like Atom and Symbol, Mathics3 variables and functions are
implemented through Python classes.
The reason that we use a class for a Mathics3 variable or a Mathics3 function is so that we can give those Mathics3 object properties and attributes.
At the lowest level of the class hierarchy is Builtin.
Lets look at a simple one:
class Head(Builtin):
"""
<dl>
<dt>'Head[$expr$]'
<dd>returns the head of the expression or atom $expr$.
</dl>
>> Head[a * b]
= Times
>> Head[6]
= Integer
>> Head[x]
= Symbol
"""
def eval(self, expr, evaluation):
"Head[expr_]"
return expr.get_head()
In the above, we have not defined an evaluation() method
explicitly so we get Expressions’s built-in evaluation()
method.
A feature of the Builtin class is the convention that its provides
a convention by which “eval” methods of the class can be matched
using the method’s name which must start with “eval” and a pattern
listed in the method’s doc string. This is used in the example above.
Here, Head has one parameter which is called expr. Note that in
the Python method there is also expr variable it its method
signature which is listed right after the usual self method that you
find on all method functions.
At the end is an evaluation parameter and this contains definitions and the context if the method needs to evaluate expressions.
Predefined Class¶
Just above Builtin in the Mathics3 object class hierarchy is
Predefined.
Some Mathics3 values like True are derived from Predefined. For example:
class True_(Predefined):
"""
<dl>
<dt>'True'
<dd>represents the Boolean true value.
</dl>
"""
name = "True"
In the above, note that the class name has an underscore (_)
appended it. We do this so as not to conflict with the Python value True. The
class variable name is used to associate the Mathics3 name.
A number of Mathics3 variables like $ByteOrdering are also derived
directly from the Predefined class. Since Python class names
cannot start with a dollar sign ($), we drop off the leading
$, in the class name, and that gives us: ByteOrdering.
As with the True example shown above, the Mathics3 name is set
using class variable name defined in the ByteOrdering
class. For example:
class ByteOrdering(Predefined):
"""
<dl>
<dt>'$ByteOrdering'
<dd>returns the native ordering of bytes in binary data on your computer system.
</dl>
"""
name = "$ByteOrdering"
def evaluate(self, evaluation) -> Integer:
return Integer(1 if sys.byteorder == "big" else -1)
The evaluate() function above is called to get the value of variable $ByteOrdering.
Test Class¶
This class is a used for Mathics3 Builtin Expression test functions
that have a suffix “Q”, AtomQ, StringQ, SymbolQ, and so on.
This class for creating builtin functions is a bit different and simpler than many of the others.
The function you define is called test() rather than some sort of eval() function.
Also, this test() function returns a Python Boolean value rather than some sort of Expression type.
The class takes care of converting this into SymbolTrue or SymbolFalse.
Here is the abbreviated code for AtomQ:
class AtomQ(Test):
"""
Docstring with links, definition, examples, etc.
"""
summary_text = "test whether an expression is an atom"
def test(self, expr) -> bool:
return isinstance(expr, Atom)
Operator¶
PrefixOperator and PostFixOperator¶
BinaryOperator and UnaryOperator¶
SympyConstant, MPMathConstant, and NumpyConstant¶
SympyFunction and MPMathFunction¶
Which class should be used for a Mathics3 Object?¶
To define a Mathics3 constant based on a Sympy constant, e.g.
InfinityuseSympyConstantTo define Mathics3 constants based on a mpmath constant, e.g.
Glaisure, useMPMathConstantTo define a Mathics3 constant based on a numpy constant, use
NumpyConstantTo define a Mathics3 functions based on a Sympy function, e.g.
Sqrt, useSympyFunctionTo define a Mathics3 operator use
UnaryOperator,PrefixOperator,PostfixOperator, orBinaryOperatordepending on the type of operator that is being definedTo define a Mathics3 function which returns a Boolean value e.g.
MatchQuseTestTo define a Mathics3 function that doesn’t fall into a category above, e.g.
AttributesuseBuiltinTo define a Mathics3 variable e.g.
$TimeZoneor Mathics3 Symbols, e.g.TrueusePredefinedTo define a Mathics3 atomic expression, e.g.
ImageAtomuseAtomicBuiltin